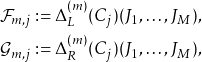At the moment, I’m primarily interested in quantum groups and their relation to integrable systems.
Let us recall that an algebra ![]() over a field
over a field ![]() is a vector space, equipped with a bilinear map
is a vector space, equipped with a bilinear map ![]() , that we call product or multiplication:
, that we call product or multiplication:
(1) ![]()
Usually, we want an algebra to be associative and unitial. This means that the map ![]() should satisfy the following conditions:
should satisfy the following conditions:
- Associativity:
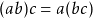 for any
for any  ,
, - Multiplicative identity: there exists an element
 such that
such that 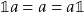 for any
for any  .
.
These two conditions can be visually represented as two commutative diagrams:
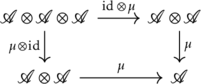
1. Associativity of ![]() ;
;
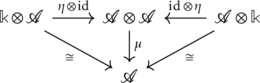
2. Existence of multiplicative identity;
where we introduced the unit map
(2) ![]()
Now we can elegantly define a (coassociative counitial) coalgebra ![]() over a field
over a field ![]() (which is a dual of an algebra) just by “reversing arrows” on a categorial level:
(which is a dual of an algebra) just by “reversing arrows” on a categorial level:
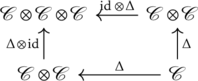
1. Coassociativity of ![]() ;
;
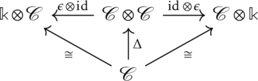
2. Existence of counit;
Here the counit is the map ![]() , dual to the unit
, dual to the unit ![]() (2). From the “physical” point of view, the coproduct
(2). From the “physical” point of view, the coproduct ![]() can be seen as an algebraic tool, allowing us to “decompose” the given system into two.
can be seen as an algebraic tool, allowing us to “decompose” the given system into two.
By adding one extra map ![]() (called an antipode) for compatibility purposes, we can also define a Hopf algebra
(called an antipode) for compatibility purposes, we can also define a Hopf algebra ![]() , which is a vector space with both algebraic and coalgebraic structures (+ antipode):
, which is a vector space with both algebraic and coalgebraic structures (+ antipode):
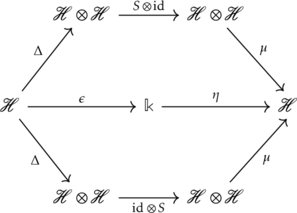
Hopf algebra
A non-commutative and non-cocommutative Hopf algebra is called quantum group [CP94] (the standard joke here is that the quantum group is not actually quantum and, moreover, it is not a group…)
Now, consider some Lie algebra ![]() , generated by the set
, generated by the set ![]() . Its Universal Enveloping Algebra
. Its Universal Enveloping Algebra ![]() can be endowed with a Hopf Algebra structure, using the so-called primitive coproduct [Tji92]:
can be endowed with a Hopf Algebra structure, using the so-called primitive coproduct [Tji92]:
(3) ![]()
The primitive coproduct can be deformed in order to build the so-called quantum deformations of a Lie algebra.
So, let ![]() be a Poisson coalgebra generated by the set
be a Poisson coalgebra generated by the set ![]() . Denote by
. Denote by ![]() , for
, for ![]() , the
, the ![]() functionally
functionally
independent Casimir functions of ![]() , i.e. the elements of
, i.e. the elements of ![]() commuting with all elements of
commuting with all elements of ![]() . Then, for
. Then, for ![]() by recursion one can define the left and right
by recursion one can define the left and right ![]() th coproduct
th coproduct ![]() , and
, and ![]() :
:
(4) 
Then one has the following
Theorem [BCR96, BR98].
Assume we are given a Poisson coalgebragenerated by the set
, a function
and fix
. Define:
and left and right Casimir functions:
(5)
where
.
Then the sets
and
are made of Poisson-commuting functions.
The abstract theorem above states that given a Poisson coalgebra and a smooth function, one can promote it to a function on its ![]() th tensor product. This function naturally commutes with two sets of functions, the left and right Casimir functions. The function
th tensor product. This function naturally commutes with two sets of functions, the left and right Casimir functions. The function ![]() is then a candidate for Hamiltonian, and the left and right Casimir functions are candidate commuting invariants.
is then a candidate for Hamiltonian, and the left and right Casimir functions are candidate commuting invariants.
To construct a classical Hamiltonian system, one needs an ![]() -degrees-of-freedom symplectic realization of the Poisson algebra
-degrees-of-freedom symplectic realization of the Poisson algebra ![]() , i.e. a map
, i.e. a map ![]() , where
, where ![]() is an open subset of a symplectic manifold, such that it preserves the commutation relations of the generators of
is an open subset of a symplectic manifold, such that it preserves the commutation relations of the generators of ![]() .
.
To build a quantum system, in turn, means to build an infinite-dimensional realization in terms of operators acting on Hilbert spaces: ![]() .
.
Therefore, the coalgebra symmetry approach [BCR96, BR98] provides us with an elegant systematic algorithm to construct an ![]() -dimensional Liouville integrable system from a given Lie algebra. Integrable systems in contemporary mathematical and theoretical physics are so important because they usually arise as “universal” limits of huge classes of nonlinear systems. Every new system found is then a source of many new results.
-dimensional Liouville integrable system from a given Lie algebra. Integrable systems in contemporary mathematical and theoretical physics are so important because they usually arise as “universal” limits of huge classes of nonlinear systems. Every new system found is then a source of many new results.
In this context, my current research aspires, in particular, to study and characterize some quantum deformations of relevant Lie algebras, to construct the (super)integrable Hamiltonian systems from those quantum deformations and to extend this construction to the discrete-time systems (for which the notion of coalgebra symmetry is slightly different, see [GL23, GLT23]).